Фундаментальный вопрос о соотношении вклада наследственности и среды в формирование количественных признаков по-прежнему остается актуальным в общей генетике, селекции, медицинской генетике человека, психологии, социологии и т.д. Не прекращается поиск новых подходов к решению проблемы эффективной селекции количественных признаков.
Методология любого исследования определяется научной парадигмой, или совокупностью исходных постулатов [1]. В данном случае она задана выделением двух основных понятий — «генотип» и «фенотип». Современная широкая трактовка генотипа как единой системы взаимодействующих наследственных элементов, определяющих пути развития организма [2], в сущности, возвратилась к исходному смыслу, вложенному в него В.Л.Иогансеном: «… Генотип — это совокупность всех наследственных задатков. Фенотип является суммой различных свойств, определяемых взаимодействием между наследственными задатками и влиянием среды» [3].
До сих пор исследования по генетике были связаны преимущественно с анализом признаков per se, что базируется на популярном постулате однозначного соответствия «ген-признак» и соответственно на представлении о генотипе как совокупности потенциальных признаков. Биометрический подход к генетическому анализу количественных признаков, как правило, не обеспечивает всех требований теории и селекционной практики по своим результатам, так как использует модели и методы, построенные зачастую на весьма неточных и неадекватных предпосылках [4, 5]. Ограниченное применение коэффициента наследуемости в селекции связано с тем, что вычисление наследуемости в широком смысле (H2) применимо только при массовом отборе, а в узком смысле (h2) — требует такой полноты знаний о генетике формирования признака, что их наличие делало бы излишним вычисление этого коэффициента [6]. Разложение фенотипической вариансы на составляющие не утвердилось в практике селекции, а используется в работах модельного характера.
Феноменологический подход, напротив, использует точные методы математической статистики для анализа количественных признаков, но не учитывает в явном виде конкретных механизмов наследования [6]. Эти подходы, не исключая друг друга, имеют свои достоинства и недостатки. Теоретическая проработка существующих подходов и методик исследований количественных признаков уже сделана в исследовании Э.Х.Гинзбурга [7] и выходит за рамки данного сообщения.
На наш взгляд, понятие «наследственные элементы» достаточно широко по смыслу и включает не только совокупность потенциальных признаков организма, но также и совокупность всевозможных взаимосвязей, которые определяются наследственной конституцией. В этом случае исходный постулат исследования формулируется следующим образом: «генотип как совокупность потенциальных признаков и взаимосвязей, обусловленных наследственностью». Тогда и понятие «паратип как ненаследуемое в организме», введенное Г.В.Сименсом [8], будет определяться как «совокупность эффектов (включая и взаимосвязи), обусловленных внешней средой». Эти постулаты определяют иную общую методологию анализа вклада наследственности и среды в фенотип, включающую целенаправленное выявление взаимосвязей, разграниченных по факторам биологической изменчивости: наследственному, средовому и т.д. [9, 10].
В гибридных популяциях паратипическая (экологическая) изменчивость количественных признаков значительно превышает генотипическую [11]. По этой причине селекционный отбор гибридов по фенотипу, равно как и последующая оценка созданных кандидатов в сорта, крайне затруднена. Для уменьшения паратипической составляющей в общей фенотипической дисперсии предлагается применять методы стандартизации условий содержания [12, 13] либо использовать фоновые индексы и поправки [14, 15]. Задача осложняется тем, что предметом отбора обычно являются отдельные хозяйственные характеристики, тогда как урожай в целом создается согласованным взаимодействием (корреляцией) этих параметров.
В данной работе использован феноменологический подход, дающий однозначную, точную и корректную интерпретацию результатов в терминах математической статистики для описания наследования количественных признаков и оценки селекционных мероприятий [6, 7]. Математический аппарат, использованный нами, был описан ранее [9, 10].
Базовой моделью исследования является классическая модель Р.Фишера, характеризующая случайное варьирование признака по закону нормального распределения [16]. Приняты следующие допущения:
1. Факторы биологической изменчивости независимы друг от друга.
2. Выборочные средние являются несмещенными оценками генеральных средних.
3. Уровни факторов не учитываются, т.е. факторы носят стохастический характер.
4. Количественное значение признака линейно зависит от колебаний фактора изменчивости.
В случае трех независимых факторов (генетического, экологического и временного) фенотипическое выражение признака выглядит следующим образом:

Учет влияния отдельных факторов осуществляется следующим образом. В случае, если значение признака определяется одномоментно или
Dx = 0, формула разложения признака приобретает вид:
Далее при полной стандартизации условий внешней среды (Ex=0) проявляется только генотипическая изменчивость организмов и
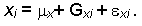
Таким образом, в данном случае вся фенотипическая изменчивость признака X определяется только эффектом i-го генотипа по данному признаку плюс случайным отклонением ![]() .
.
Аналогичные рассуждения по поводу другого количественного признака (Y) у того же объекта наблюдения приводят к формуле:
Вычисление фенотипической линейной корреляции между набором значений xj и yj дает искомое значение генотипической корреляции между признаками X и Y [17].
При стандартизации генотипов варьирование внешних условий приводит к
и коэффициент корреляции между фенотипами X и Y есть экологическая корреляция.
Динамическая (сезонная, онтогенетическая, временная) корреляция определяется как фенотипическая при
Иными словами, фенотипические корреляции признаков вызваны сопряженной изменчивостью, определяемой как алгебраическая сумма смещений (факторных эффектов) относительно константы ![]()
Очевидно, что для выявления, например, генотипической корреляции необходимо нивелировать все факторы, кроме вариабельности генотипов. Создание средовой (экологической) однородности достигается путем максимально возможной стандартизации экспериментальных условий (фитотронные камеры для растений, рацион питания для животных и т.д.). Идентичность генотипов достижима путем клонирования или создания чистолинейного генетического материала. Влияние фактора времени наблюдения можно уменьшить, если проводить все наблюдения одновременно. Остальные неучтенные факторы ослабляются рандомизацией эксперимента.
Принятие линейной аддитивной модели со случайными факторами позволяет, не прибегая к непосредственной стандартизации факторов изменчивости, условно нейтрализовать эффекты отдельных факторов путем введения соответствующих факторных поправок в конкретные наблюдаемые значения признака и на этой основе выявлять искомые взаимосвязи. Такой подход при расчете генотипической корреляции приведен на рисунке 1. Большим эллипсом обозначено корреляционное поле для общей фенотипической корреляции без внесения факторных поправок, малые эллипсы — корреляционные поля в отдельных выборках и в объединенной выборке после учета факторных поправок.
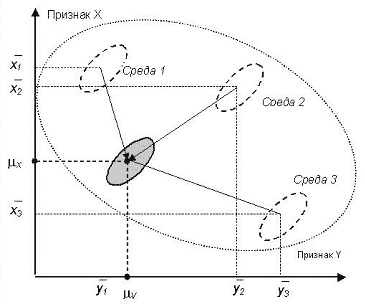
Рис. 1. Схема внесения факторных поправок при объединении разнородных данных для оценки генотипической корреляции между признаками X и Y (обозначения в тексте).
В рандомизированной группе наблюдений n генотипов в m экологических ситуациях конкретная последовательность операций вычисления генотипической корреляции между признаками X и Y следующая:
а) вычисление среднего значения признака по каждой экологической ситуации
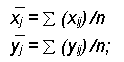
б) определение общего среднего (![]() ) по каждому признаку
) по каждому признаку
в) определение величины линейного экологического смещения выборок
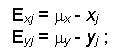
г) внесение линейной факторной (в данном случае экологической) поправки в выборки данных даст n совокупностей xj и yj:
д) объединение всех значений xj и yj в общую выборку по признакам X и Y, в которой изменчивость обусловлена компонентой Gj
Коэффициент линейной корреляции между X и Y после внесения поправок на генотипический фактор дает искомый коэффициент генотипической корреляции.
Выявление экологической корреляции между X и Y происходит подобным образом, но с внесением соответствующих генотипических поправок Gxj и Gyj.
Конкретное применение данного подхода проиллюстрируем на примере корреляционного анализа количественных признаков мягкой пшеницы (Triticum aestivum L.) по результатам, полученным в ходе осуществления селекционно-генетической программы «ДИАС» [18]. Использованы числовые данные по следующим признакам продуктивности:
- Число дней от появления всходов до колошения (ЧДВК).
- Общее число стеблей на растении (ЧС).
- Длина главного стебля (ДГС).
- Длина нижнего (первого надземного) междоузлия.
- Длина колоса (ДК).
- Число зерен в колоске (ЧЗКК).
- Вес зерна с растения (ВЗР).
- Вес 1000 зерен (ВТЗ).
Участниками программы исследовано 15 сортов в 8 различных экологических зонах в течение 2 лет (1974-1975). Повторность наблюдений в каждом пункте — восьмикратная. Подробное описание эксперимента дано в коллективной монографии В.А.Драгавцева и др. [18]. Уровень заполнения матрицы данных близок к 100%, что обеспечило общий объем выборки в более 30000 чисел. Приближение распределения данных к нормальной форме достигали путем логарифмирования параметров. В случае объединения данных по годам использована межгодовая поправка. Вычисления проводились по приведенной выше схеме. Для устранения эффекта случайного компонента ![]() определение
определение ![]() проводили по внутрисортовым либо экологическим средним.
проводили по внутрисортовым либо экологическим средним.
На рисунках 2-4 представлены результаты корреляционного анализа признаков, отражающих основные морфолого-функциональные элементы продуктивности: продолжительность онтогенеза, кустистость растений, интенсивность вегетативного прироста на разных этапах развития, интенсивность развития генеративных органов и параметры налива зерна.
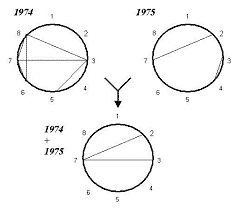
Рис. 2. Фенотипическая корреляция количественных признаков пшеницы («ДИАС»).
1 — продолжительность периода «всходы-колошение»; 2 — общее число стеблей; 3 — длина главного стебля; 4 — длина нижнего междоузлия; 5 — длина колоса; 6 — число зерен в колоске; 7 — общий вес зерна с растения; 8 — вес 1000 зерен ——- 0,60 < r ≤ 0,80
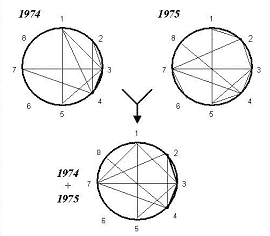
Рис. 3. Генотипическая корреляция количественных признаков пшеницы («ДИАС»).
1 — продолжительность периода «всходы-колошение»; 2 — общее число стеблей; 3 — длина главного стебля; 4 — длина нижнего междоузлия; 5 — длина колоса; 6 — число зерен в колоске; 7 — общий вес зерна с растения; 8 — вес 1000 зерен. 0,80 < r ≤ 1,00. —— 0,60 < r ≤ 0,80
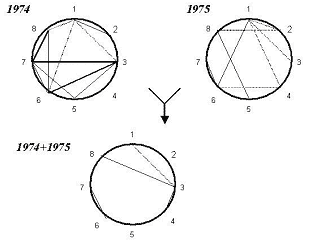
Рис. 4. Экологическая корреляция количественных признаков пшеницы («ДИАС»).
1 — продолжительность периода «всходы-колошение»; 2 — общее число стеблей; 3 — длина главного стебля; 4 — длина нижнего междоузлия; 5 — длина колоса; 6 — число зерен в колоске; 7 — общий вес зерна с растения; 8 — вес 1000 зерен. 0,80 < r ≤ 1,00. 0,60 < r ≤ 0,80
Общее число фенотипических корреляций существенного уровня (r > 0,60 при p < 0,001) сильно варьировало по годам от 6 в 1974 до 2 в 1975. Следует отметить, что все они положительны, а подавляющее большинство из выявленных связей очень мало и они не достигают установленного критического уровня (0,60). Не обнаружено ни одной связи высокого (более 0,80) уровня. Объединение данных двух лет не привело к росту числа связей. Напротив, большинство корреляций при этом исчезает. Это свидетельствует о том, что имеет место феномен ослабляющего влияния неучтенных факторов [19]. Добавим, что причины фенотипической сопряженной изменчивости признаков при этом остаются вне поля зрения, так что дать адекватную содержательную интерпретацию нестабильности корреляций невозможно, за исключением общих спекуляций на тему эффектов тех или иных погодных особенностей в разные годы наблюдений.
Внесение экологических факторных поправок с целью выявления генотипической корреляции выявило следующее (рис. 3). Общее количество связей, превзошедших пороговый уровень «существенности» в 0,60, составило в 1974 и 1975 гг. по 9 в каждый год, причем все они положительны. Это свидетельствует о проявлении генотипических связей, которые были скрыты в фенотипе и стали заметны благодаря очистке от экологических «наслоений». При объединении данных по годам число генотипических связей выросло до 11. Очевидно, это связано с еще большим устранением эффектов экологических факторов, а именно устранением эффектов погодных различий. Характерно, что большинство из выявленных генотипических взаимосвязей остаются стабильно высокими из года в год. Более того, при объединении данных вдвое растет число связей особо высокого (более 0,80) уровня. Все это свидетельствует об эффективности приема внесения экологических поправок для «очистки» закономерностей генотипической сопряженной изменчивости. Подчеркнем, что выделение генотипических коррелятивных связей достигнуто в условиях, когда паратипический информационный «шум» многократно (в 3-50 раз) превышает генотипический «сигнал», по собственной оценке авторов исходных данных [18]. Использованный в программе «ДИАС» набор не родственных между собой сортов изучался в экологически достаточно удаленных друг от друга зонах (около 1000 км по географической широте и более 3000 км по долготе). Пестрота условий географических точек и лет испытания плюс генетические различия сортов на уровне фенотипа «смазали» корреляционные связи признаков. Введение факторных поправок позволило установить генетические корреляции, что существенно как для построения модели сорта, так и для анализа результатов их испытания.
Внесение генотипических поправок выявляет совершенно иную картину (рис. 4). Несмотря на то, что благодаря факторным поправкам выявляются многочисленные экологические взаимосвязи (в 1974 г. — 11, а в 1975 г. — 7), вместе с положительными наблюдаются и отрицательные корреляции. Экологически стабильны лишь две пары признаков: число дней до колошения — длина стебля и число зерен колоса — вес зерна одного растения. Прямое объединение данных двух лет привело, с одной стороны, к общему падению числа связей существенного уровня (до 4), а с другой — к полному исчезновению связей особо высокого уровня. Большинство связей не стабильны, вплоть до того, что меняют знак на противоположный в разные годы (например: срок колошения с числом побегов кущения или с числом зерен в колосе).
Все это означает, что благодаря стандартизации по генотипам выявляются экологические корреляции, обусловленные почвенными и погодными различиями. При прямом объединении данных разных лет начинает заметно проявляться действие еще одного, третьего фактора изменчивости. По-видимому, этим фактором являются процесс онтогенеза пшеницы (в частности, условия прохождения критических фаз развития) и его взаимодействие с параметрами экологических ситуаций в разные годы. На это указывает то, что в обоих случаях смены знака участвует временной параметр — число дней от всходов до колошения (ЧДВК). Выделение в чистом виде экологически обусловленных корреляций признаков важно для изучения пластичности генотипов, их адаптации к условиям среды.
Известно, что влияние факторов изменчивости гораздо сильнее отражается на корреляциях признаков, чем на их абсолютных значениях [19]. Это связано с широко известным феноменом канализации или буферности процессов формирования признаков и, в частности, с сохранением параметров гомеостаза организма [20]. Следовательно, можно с полным основанием говорить о генотипических и экологических корреляциях, обеспечивающих (обслуживающих) в конечном итоге адаптацию и нормальную жизнедеятельность организмов в различных условиях среды. Поэтому исследования корреляций представляют интерес при создании адаптивных генотипов и получении требуемых характеристик продуктивности.
Очевидно, что в данном случае биологическая специфика выбранного объекта селекции не играет роли. Метод факторных поправок одинаково успешно может работать на любых объектах. Однако необходимо отметить один существенный момент, относящийся к реальному характеру селектируемых признаков. В случае наиболее сложных параметров, таких, как общая продуктивность, очевидно, необходимо учитывать эффект взаимодействия факторов. Если же признаки относительно просты (например, отдельные элементы продуктивности, содержание отдельных химических веществ и т.п.), то их формирование обеспечивается единым механизмом (нет «забуференности» внешними отрицательными и положительными обратными связями) и они относительно слабо вовлекаются в процесс канализации. Корреляционный анализ таких признаков по отдельным факторам изменчивости наиболее эффективен.
Другой существенный момент заключается в следующем. Принято считать, что для адекватной интерпретации результатов линейного корреляционного анализа необходимо, чтобы форма распределения экспериментальных данных была близка к нормальной. Однако, за исключением случаев грубых артефактов, принципиальная важность этого требования, как правило, преувеличивается. Практика многих исследований показывает, что величина r мало чувствительна к асимметрии распределения. Логарифмическая трансформация числовых данных, многократно уменьшая коэффициент асимметрии, влияет на величину r лишь на уровне сотых долей [21]. Более того, огрубление исходной информации при вычислении ранговой корреляции и корреляционного отношения позволяет в большинстве случаев преодолеть ограничения, налагаемые асимметрией.
Возвращаясь к началу статьи, напомним, что реальный прогноз фенотипического значения количественного признака чрезвычайно затруднен. И дело здесь не в слабой методологической и методической базе, а в сложности самих объектов селекции и в недооценке роли многих неучтенных факторов, которые, наряду с генотипом, определяют изучаемые признаки. Понадобился напряженный целенаправленный труд многих научных коллективов на протяжении ряда лет, чтобы в итоге прийти к обоснованному заключению, что паратипический «шум» в формировании рассмотренных выше признаков продуктивности у пшеницы многократно превышает генотипическую компоненту [18]. И это без учета вклада процессов онтогенеза, еще одного важнейшего и сложнейшего фактора. Пока что дело ограничивается лишь включением этого фактора в общую блок-схему формирования признака [22]. Создание соответствующего биометрического аппарата для более точного прогноза значения количественного признака — дело будущего.
Предлагаемая методология делает возможным еще один вариант прогноза. Речь идет не об абсолютном, а об относительном экологическом либо генотипическом прогнозе селектируемого признака по комплексу коррелятивных связей. Метод линейных факторных поправок — лишь первое, наиболее грубое приближение, но уже в таком виде он демонстрирует свою результативность. Принятые допущения в большинстве случаев не противоречат реальным ситуациям, поэтому предварительная линейная трансформация исходных числовых данных позволяет провести дальнейшую детализацию исследования, например, факторный анализ, выявление корреляционных плеяд и т.д. Не претендуя на исчерпывающую полноту результатов, этот прием может быть полезным также и при сравнении различных генотипов в селекции.
Таким образом, излагаемый здесь метод может найти широкое применение и в процессе создания новых сортов, и при их экологическом испытании.
Литература
- Краткая философская энциклопедия. М.: Прогресс, 1994. C. 332.
- Инге-Вечтомов С.Г. Генотип // Биологический энциклопедический словарь. М.: Сов. энцикл. 1989. С. 126.
- Иогансен В.Л. Элементы точного учения об изменчивости и наследственности. М.;Л.: Сельхозгиз, 1933. 410 с.
- Hiorth G.E. Quantitative Genetik. Berlin а.о.: Springer-Verlag, 1963. P. 2-3.
- Хатт Ф. Генетика животных. М.: Колос, 1969. С. 281.
- Гинзбург Э..Х., Никоро З.С. Разложение дисперсии и проблемы селекции. Новосибирск: Наука, 1982. 168 с.
- Гинзбург Э.Х. Описание наследования количественных признаков. Новосибирск: Наука, 1984. 250 с.
- Siemens H.W. Konstitutions- und Vererbungspathologie. Berlin, 1921. (Цит. по [3, С. 198]).
- Скуридин Г.М., Багинская Н.В. Новый подход в корреляционном анализе количественных признаков // Сб. тр. конф., посвященной 90-летию со дня рождения А.А.Ляпунова. 8-11 октября 2001 г. Новосибирск, 2001. http://www-sbras.nsc.ru/wc/Lyap2001/.
- Skuridin G.M., Baginskaya N.V. Correlation database analysis using the method of factor corrections // Proc. Intern. Conf. «Genetic collections of isogenic and alloplasmic lines». Novosibirsk: Inst. Cytol. and Genet. 2001. P. 280-284.
- Гужов Ю.Л., Гнейм А.Р. Закономерности варьирования количественных признаков у гороха, обусловленные модификациями и генетическими различиями // Генетика. 1982. Т. 18, № 2. С. 82-99.
- Литун П.П. Приемы уменьшения фенотипической изменчивости и ее компонентов на разных этапах отбора в селекции // Генетика количественных признаков сельскохозяйственных растений. М., 1978. С. 93-100.
- Литун П.П., Манзюк В.Т., Барсукова П.Н. Методы идентификации генотипов по продуктивности растений на ранних этапах селекции // Проблемы отбора и оценки селекционного материала. Киев: Наук. Думка, 1980. С. 16-28.
- Драгавцев В.А., Шкель Н.Н., Ничипоренко Н.Н. Задачи идентификации генотипов растений по фенотипам // Вопросы селекции и генетики зерновых культур: Сб. науч. тр. М., 1983. С. 291-298.
- Мартынов С.П., Крупнов В.А. Экспериментальная проверка эффективности селекционного индекса на яровой пшенице // Цитология и генетика. 1982. Т. 16, № 4. С. 36-39.
- Fisher R.A. The correlation between relatives on the supposition of Mendelian inheritance // Trans. Roy. Soc. Edinburgh. 1918. P. 399-433. (Цит. по [6, С. 16]).
- Драгавцев В.А. Методы оценки генотипической, генетической и экологической корреляции количественных признаков в растительных популяциях // Генетический анализ количественных и качественных признаков с помощью математико-статистических методов. М., 1973. С. 45-47.
- Драгавцев В.А., Цильке Р.А., Рейтер Б.Г. и др. Генетика признаков продуктивности яровых пшениц в Западной Сибири. Новосибирск: Наука, 1984. 230 с.
- Ефимов В.К., Галактионов Ю.К., Галактионова Н.С. О связи величин коэффициентов корреляции и вариации с абсолютными значениями признаков // Журн. общей биологии. 1977. Т. 38, № 1. С. 24-26.
- Жученко А.А. Экологическая генетика культурных растений. Кишинев: Штиинца, 1980. С. 77-79.
- Куршакова Ю.С. Корреляционный и регрессионный анализ в практическом применении // Теория отбора в популяциях растений: Сб. науч. тр. Новосибирск: Наука, 1976. С. 49-57.
- Драгавцев В.А., Литун П.П., Шкель Н.М., Нечипоренко Н.Н. Модель эколого-генетического контроля количественных признаков растений // Докл. АН СССР. 1984. Т. 274, № 3. С. 720-723.
Г.М.Скуридин, н.с.
С.Ф.Коваль, к.б.н., с.н.с.
Институт цитологии и генетики СО РАН, Новосибирск

